Overview
Array rods are a length-based manipulative with each of the centimeter-based lengths color-coded to match a specific length. For example, below all the 10s are blue, 9s are purple, etc. On one side of each array rod is the printed numeral and the other side includes the discrete counts of objects for that number. The rods can be arranged to form an array to aid students in understanding the row/column structure, or used for basic addition/subtraction.


MakerSpace Files
Array rods will need to be 3D printed. Below are estimates for the amount of material, along with recommended color schemes. The estimated costs are conservative estimates and you may be able to find less expensive filament.
Click here to download a standard set from Makerworld (Bambu Printers).
Click here to download the set of files in Thingiverse.
Each link includes stl files for 3D printers, but the Makerworld link includes profiles for direct printing on the Bambu brand of printers.
Note: If you have not read the tutorial post on MakerSpace Manipulatives, please do so.
| Color Scheme We Use | grams of PLA | Cost ($18 / KG | Time w/ 0.6mm nozzzle | |
| 1s (n = 20) | White | 4.45 | $0.08 | 17 min |
| 2s (n = 12) | Gray | 7.18 | $0.13 | 23 min |
| 3s (n = 12) | Yellow | 10.99 | $0.20 | 33 min |
| 4s (n = 12) | Light Green | 14.65 | $0.26 | 43 min |
| 5s (n = 12) | Red | 18.35 | $0.33 | 51 min |
| 6s (n = 12) | Light Blue | 22.10 | $0.40 | 1 hr 3 min |
| 7s (n = 12) | Pink | 26.14 | $0.47 | 1 hr 12 min |
| 8s (n = 12) | Dark Green | 29.50 | $0.53 | 1 hr 21 min |
| 9s (n = 12) | Purple | 33.56 | $0.60 | 1 hr 32 min |
| 10s (n = 12) | Dark Blue | 36.61 | $0.66 | 1 hr 42 min |
| Total (n = 126) | 203.53 | $3.66 | 9 hr 37 min |
Examples of Use
Composing/Decomposing Numbers in Addition
Students can use array rods to learn how to compose/decompose numbers when learning to add with regrouping. In the below example, a two-digit number and one-digit number are added together. It’s important to do these types of numbers first as having two two-digit numbers adds a layer of complexity and students may not see the connection between decomposing the ones and making 10s.
Students can flip over the number to see the dots and think of how a 9 can be decomposed into a 6 and 3. By having students write and draw on their paper, they will begin to make connections between the concrete/pictorial and the symbolic.

Multiplication Facts & Properties
Arrays are an extremely useful tool for helping students learn basic multiplication/division. However, most tools involve getting EACH INDIVIDUAL ONE and arranging into the rows or columns. Students can use array rods to quickly create an array. In the below example, a child can create a 7 by 8 array to illustrate 7×8. Children often have difficulty learning the Distributive Property, but this manipulative can simplify the process by guiding the child to create different pairs of facts that can be added to get 7×8 (see four steps below).

Following such types of activities, children can then use the Distributive Property to learn multiplication by 7s – as 7s facts tend to be difficult for children to learn. Rather, children can use this property to break the 7s into 5s and 2s as a simple way of meaningfully memorizing 7s multiplication fats. In a similar manner, children can use the array rods to learn different multiplication properties and apply this to meaningfully memorizing their different multiplication facts.
Multi-Digit Multiplication
Many children learn the standard algorithm without any manipulatives or corresponding number sense. As a result, they make several mistakes because they do not understand the values they are computing with the algorithm.
Array rods (with the decade expansion pack) can be used to support meaningful understanding of multi-digit multiplication. Preferably, children use the area model (with the manipulatives) to learn the box model and then transition to the partial products model:
- Area Model: This is often confused with the box model (and they are related) but is distinct in that the area model shows the actual area you are computing. This is often used with manipulatives or grid paper (or both). You do not need symbolic notation to model this but it will make learning multiplication more meaningful.
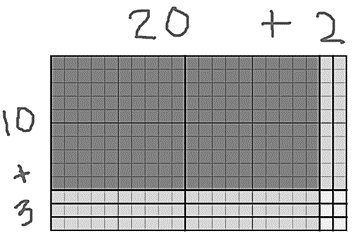
- Box Model (algorithm): The box model is a quasi pictorial-symbolic representation where you do not need the sections to be proportional (like the area model above). You are more explicitly modeling partial products. HOWEVER, if this model is not paired with the area model (before) and the partial products model (after), there is a risk of it becoming an “easy to way to get the answer” approach instead of a meaningful one.

- Partial Products Model (algorithm): In a recent pilot project, we found that students reporting more exposure to (and use of) this model had higher multiplicative reasoning than any other approach. When paired with use of array rods (as shown in the video below), the partial products model is an excellent way to support upper elementary students’ meaningful learning of multi-digit multiplication.
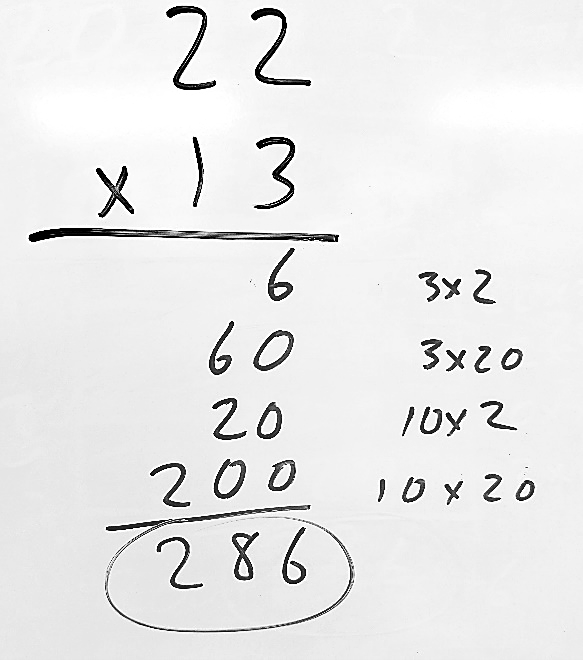
It is important to note how this approach is different from the standard algorithm. First, each product is written separately with each multiplication expression to the side. This is to reinforce the connection to place value in the numbers and a better understanding of partial products. Quite often, students get confused by how many numbers they need to multiply (anyone with traumatic memories of FOIL may understand). The partial products model, paired initially with array rods, supports meaningful connections for students who may be at very different levels of multiplicative reasoning.
Multi-Digit Division
The long division algorithm has traumatized children for over 200 years. This is because the rules they are taught to use do not always make mathematical sense. We advocate use of the partial quotients algorithm as a way for children to construct meaning of multi-digit division. It looks quite similar to long division but emphasizes properties that students use in multi-digit multiplication (thus making it make more sense).
The video below illustrates the partial quotients approach with the array rods. By pairing the two, children will begin to make better sense of division, its relationship to multiplication, and need to “see” the visualization less and less.
More to come…

Pingback: Area Sliders – Extended Reality Initiative